4.______________________________
In Chapter 2, we developed an understanding of how to determine the rate and amount of energy coming from the sun. We introduced in that section the concept of the cosine effect or cosine loss representing the difference between the amount of energy falling on a surface pointing at the sun, and a surface parallel to the surface of the earth.
In order to collect solar energy here on the earth, it is important to know the angle between the sun’s rays and a collector surface (aperture). When a collector is not pointing (or more exactly, when the collector aperture normal is not pointing) directly at the sun, some of the energy that could be collected is being lost.
In this chapter, we develop the equations to calculate the angle between a collector aperture normal and a central ray from the sun. This development is done first for fixed and then for tracking collectors. These equations are then used to provide insight into collector tracking and orientation design by predicting the integrated solar radiation energy that is incident on the collector aperture and could be collected. These concepts will be developed with the following outline:
4.1 Aperture-Sun Angles; The Angle of Incidence
In Chapter 3, we defined the sun's position angles relative to earth-center coordinates
The other angle of importance, discussed in this section is the tracking angle,
In this section we derive expressions for the angle of incidence for both fixed-axis and single-axis tracking apertures. We also derive equations for the tracking angle for both single-axis and two-axis (full) tracking apertures. Zimmerman (1981) has reviewed a number of sun pointing programs and evaluated their accuracy
4.1.1 Fixed (non-tracking) Apertures
The cosine of the angle of incidence for an arbitrarily oriented surface or aperture that does not track may be described in terms of the orientation of the collector and the solar altitude and azimuth angles. An expression for this is developed by taking the scalar or dot product of a unit vector
S pointing from the collector aperture toward the sun and a unit vector N normal to the collector aperture. The unit vector S was defined in Chapter 3 by Equation (3.9) in terms of direction cosines given in Equation (3.10) which are functions of the solar altitude and azimuth angles.To define
N using the same axes, we will define an aperture tilt angle
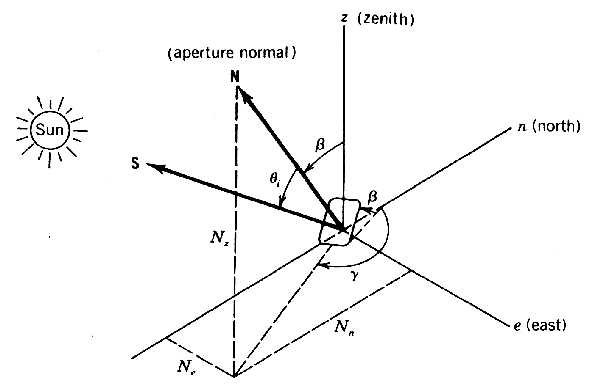
Figure 4.1 A fixed aperture with its orientation defined by the tilt angle
The cosine of the angle between a sunray and the aperture normal is the dot product of these two unit vectors:
Applying Equations (3.10) and (4.1), we have for the cosine of the angle of incidence for a fixed aperture:
It is sometimes useful to write Equation (4.3) in terms of latitude, declination, and hour angle rather than solar altitude and azimuth. Using Equation (3.14), (3.15) and (3.16) does this, and the result is
(4.4)
Special cases of Equation (4.3) are often of interest.
For horizontal apertures, the tilt angle is zero and Equation (4.3) becomes
(4.5)
For vertical apertures, Equation (4.3) becomes
(4.6)
and for a tilted aperture facing south, we have
(4.7)
4.1.2 Single-Axis Tracking Apertures
Certain types of concentrating collector are designed to operate with tracking rotation about only one axis. Here a tracking drive system rotates the collector about an axis of rotation until the sun central ray and the aperture normal are coplanar. Figure 4.2 shows how rotation of a collector aperture about a tracking axis r brings the central ray unit vector S into the plane formed by the aperture normal and the tracking axis. The angle of incidence is also shown. The tracking angle
measures rotation about the tracking axis r, with
when N is vertical.

Figure 4.2
A single-axis tracking aperture where tracking rotation is about the r axis. The sun ray vector S is kept in the plane formed by the r axis and the aperture normal N by this rotation.To write expressions for
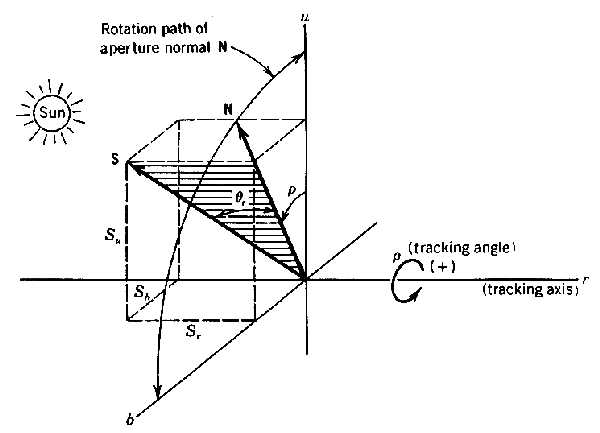
Figure 4.3
Single axis tracking system coordinates. The collector aperture rotates about the r axis, where N is a unit vector normal to the collector aperture.Inspection of this figure reveals that both
Remembering that S is a unit vector, the cosine of the angle of incidence is
In the sections that follow we develop equations for and
, first for cases where the tracking axis is arbitrarily oriented but still parallel to the surface of the earth, and then for cases where the tracking axis is inclined relative to the surface of the earth. Both cases require a coordinate transformation.
Horizontal Tracking Axis. To describe this category of tracking schemes, we must rotate the u, b, and r coordinates by an angle from the z, e, and n coordinates that were used to describe the sun ray unit vector S in Equation (3.10). Since the tracking axis is to remain parallel to the surface of the earth, this rotation takes place about the z-axis as shown in Figure 4.4, with the u and z-axes coincident. Note that this rotation is in the negative direction based on the right-hand rule. The rotated direction cosines of S take the form

Figure 4.4
Rotation of the u, b, r coordinates from the z, e, n coordinates about the z-axis. Diagram shows view looking downward on the surface of the earth.Solving and substituting into Equation
(4.8), we have for the general case of a collector aperture tracking about a single, horizontal axis, the tracking angleand from Equation (4.9), the angle of
A special case of this equation commonly found in practice is when the tracking axis is oriented in the north-south direction
(4.13)
and
(4.14)
When the tracking axis is oriented in the east-west direction, Equations (4.11) and (4.12) become
(4.15)
and
(4.16)
Tilted Tracking Axis. Starting with the arbitrarily oriented horizontal tracking axis r from the previous section, we now tilt this axis from the horizon by an angle as shown in Figure 4.5. Again, describing the direction cosines for the sunray unit vector in these new coordinates, we take a column matrix describing the solution to Equation (4.10) and rotate it in a positive direction through an angle
. The direction cosines are found by solving

Figure 4.5
Rotation of the collector coordinates about the horizontal axis b.Applying the solution of this to Equations
(4.8) and (4.9), we haveand
If the tracking axis r is tilted toward the south as is often done, the equations above simplify on setting to 180 degrees.
Offset Aperture In some tracking designs, the collector aperture is offset relative to the tracking axis by an angle as shown in Figure 4.6. For this design, the tracking angle
is still as computed by Equation (4.18) since the aperture normal N remains in the plane formed by the tracking axis r and the sunray vector S. However, the angle of incidence
is no longer that computed by Equation (4.19). The angle of incidence for this case is simply the sum of the angle of incidence found in Equation (4.19) and the aperture offset
. Appropriate signs must be used for each. The aperture offset
is considered positive when offset counterclockwise (based on the right-hand rule) about the b axis. The sign for the angle found by Equation (4.19) would be the same as the sign of Sr found in Equation (4.17).

Figure 4.6 Tracking with the collector offset with respect to the tracking axis by an angle
Two special cases of Equation
(4.18) and (4.19) that occur in practice are the case of the vertical collector and the collector whose tracking axis is tilted toward the south at the local latitude angleVertical Tracking Axis For the vertical tracking axis case, the tracking axis become collinear with the zenith axis and Equations
(4.18) and (4.19) simplifies to
(4.20)
where by convention the tracking angle is counterclockwise about the zenith.
Vertical Tracking Axis With Offset Aperture In some designs the collector aperture is offset by an angle relative to the vertical tracking axis. In this case, the tracking angle and angle of incidence become
(4.21)
where when the tracking axis is aligned with the plane of the aperture. Examples of this scheme are large concentrator arrays floating in a pond and arrays on circular railroad-like tracks.
Tracking Axis Tilted at Latitude Angle. When the tracking axis is tilted from the horizon by the latitude angle, toward the south, it is parallel to the earth’s rotational pole and points toward the pole star, Polaris. Called either a polar mounting or an equatorial mounting, the solution of Equations (4.18) and (4.19) for this case reveals two important aspects of this class of mount. Substituting the latitude angle for the tilt angle
and then substituting Equations (3.17) and either (3.18) or (3.19) to replace the solar altitude and azimuth with latitude, declination, and hour angle does this.
An equivalent and analytically easier, procedure is to rotate the z, e, ,n coordinates about the e axis by the latitude angle . This gives direction cosines of the central ray unit vector S in terms of our u, b, r coordinates.
Starting with Equation (3.10) and casting the direction cosines of S in terms of latitude, declination, and hour angles through application of Equation (3.14), (3.15) and (3.16), these are substituted into Equation (4.22) for Sz, Se, and Sn. Taking the definition of and
from Equations (4.8) and (4.9) and after considerable simplification, we have for the tracking angle and angle of incidence for the polar mount:
(4.23)
Since the hour angle changes at the exact rate of 15 degrees per hour, a simple constant speed "clock drive" can be used to turn the aperture about the tracking axis.
Furthermore, the angle of incidence, which is the declination angle, varies by only 23.45 degrees throughout the year, giving a minimum value to the cosine of the angle of incidence of 0.917. The result is a single-axis-tracking collector with a maximum cosine loss of 8.3% at the solstices.
Of more importance is the fact that the declination angle changes very slowly with a maximum rate of about 0.4 degree per day at the equinoxes. This gives rise to the possibility of periodic adjustments of the angle between the collector aperture and the tracking axis in order to maintain a small angle of incidence.
4.1.3 Two-axis Tracking, Apertures
With two-axis tracking, a collector aperture will always be normal to the sun. Therefore the cosine effect does not come into play and;
(4.24)
For aiming an aperture toward the sun at all times, rotation about two axes is always required. Two types of tracking mechanism are commonly in use for this purpose: azimuth / elevation tracking systems (also called az-el systems) and polar or equatorial tracking systems.
Azimuth / Elevation Tracking. With azimuth / elevation tracking, the collector aperture must be free to rotate about the zenith axis and an axis parallel to the surface of the earth. The tracking angle about the zenith axis is the solar azimuth angle (A), and the tracking angle about the horizontal axis is the solar altitude angle
, as defined in Equations, (3.18), (3.19) and (3.17) respectively.
Of primary interest to the designer of a two-axis tracking system is the rate at which these angles change called the slew rate. For the azimuth / elevation system, the rates of change of both the azimuth and elevation angles are not constant and depend on the location, time of day, and season. An expression for the slew rate about the horizontal axis may be found by taking the derivative of Equation (3.17) with respect to time. If we neglect the very slow variation in declination angle, the result is
(4.25)
The slew rate about the vertical axis is found similarly from Equation (3.18) and is
(4.26)
Figure 4.7 shows the variation of these slew rates at a specific location. Note the very high azimuth slew rates required near the summer solstice at noon. This must be considered in the design of tracking drive mechanisms and tracking controls.

Figure 4.7 Variation in the rate at which the solar azimuth and altitude angles change for three representative days. The latitude is 32 degrees for this example.
Polar (Equatorial) Tracking
. For polar or equatorial tracking systems, one axis of rotation is aligned parallel to the earth’s rotational pole, that is, aimed toward the star Polaris. This gives it a tilt from the horizon equal to the local latitude angle. As described in the previous section, the tracking angle about the polar axis is equal to the sun’s hour angleThe slew rate about the polar axis is constant at 15 degrees per hour. The slew rate about the declination axis is very slow, giving rise to the possibility of incremental adjustment. The rate is dependent on the time of year and can be found by taking the derivative of Equation (3.7) with respect to time. The result is
(4.27)
which give a maximum tracking rate of 0.0163 degrees per hour (0.28 mrad/h) at the equinoxes. With many types of concentrating collector optics, incremental adjustment rather than a continuous tracking motion may do this slow rate of tracking.
4.2 Collector Aperture Irradiance and Solar Radiation Energy
The aperture area of a solar collector is the area of the opening into which insolation passes. This is the area one would obtain by direct measurement and does not include any area reduction due to angle of incidence effects or shadowing. After passing through the aperture, that insolation may be concentrated or absorbed as is the case for the flat-plate collector.
4.2.1 Irradiance on a Collector Aperture
The rate at which solar energy enters a collector aperture, divided by the aperture area is called the aperture irradiance. This is usually made up of beam aperture irradiance and diffuse aperture irradiance. The angle of incidence between the aperture normal and a central ray of the sun depends on the time of day, the day of the year, the location and orientation of the aperture, and whether it is stationary or tracks the sun’s movement about one or two axes as described above.
For concentrating solar collectors, the solar designer is only interested in the direct (beam) irradiance on the aperture since most concentrating collectors only concentrate the direct irradiance. For flat-plate solar collectors, the global (total) aperture irradiance is of interest since flat-plate collectors are able to absorb both direct and diffuse irradiance.
Direct (Beam) Aperture Irradiance - In Chapter 2, Section 2.1 we discussed the rate of energy falling on a horizontal surface outside the earth’s atmosphere and found that it was reduced by the cosine of the angle between the sun and a line normal to the surface. This was called the cosine effect or sometimes the cosine loss and is described by Equation (2.2) for the extraterrestrial horizontal surface.
The collector aperture irradiance, the rate at which solar energy is incident on the aperture per unit aperture area, may be found from the irradiance measurements discussed to this point. If only the beam component of insolation is of interest (as with most concentrating collectors), the aperture irradiance for beam insolation may be calculated as:
where is the beam normal irradiance and
is the angle of incidence. Here, the reader can see here the importance of being able to calculate the angle of incidence
Global (Total) Aperture Irradiance - The global aperture irradiance is the sum of the beam plus diffuse and reflected irradiance. The beam irradiance is the same as given in Equation (4.28). The diffuse (sky) and the reflected (ground) irradiance are apportioned by the fraction of the hemispherical view by the aperture above or below the horizon.
where is the diffuse (scattered) irradiance,
the global (total) irradiance falling on a horizontal surface, the angle
is the tilt angle of the aperture relative to the horizontal and
the reflectance of the surrounding surface.
Note here that if the aperture is horizontal, the angle , and only the diffuse (sky) irradiance contributes to the global irradiance. If the aperture is vertical,
and both the diffuse (sky) irradiance and the irradiance reflected from the ground contribute equally.
Data for both direct normal irradiance and global horizontal irradiance are generally available in the TMY2 and other databases (see Chapter 2). The diffuse irradiance can be calculated using Equation (2.9). A table of various ground surface reflectance values is provided in the Appendix.
Using the appropriate equation for angle of incidence derived in Section 4.1 above, the solar designer can now calculate how much global (direct) solar energy is coming to a collector aperture at any time, date and location, and with any orientation or tracking design.
4.2.2 Solar Radiation Energy on a Collector Aperture
The aperture solar radiation energy is the irradiance on the aperture summed (integrated) over a period of time, usually a full day. In some texts and figures in this book, solar radiation energy is also called irradiation.
As in Equation (2.3), the daily beam (direct) aperture solar radiation energy is found by integrating the beam aperture irradiance given in Equation (4.28), from sunrise to sunset
(4.30)
Likewise, the daily global (total) aperture solar radiation energy is found by integrating the global aperture irradiance given in Equation (4.29), from sunrise to sunset
(4.31)
Also of interest are the monthly and annual solar radiation available to a collector. These are obtained by summing values of daily aperture solar radiation energy over the appropriate period.
The expressions developed so far may be used, along with TMY insolation data to predict the solar resource available to collectors using different tracking methods and orientations. Figure 4.8 and 4.9 show the results of such a study made for Albuquerque, NM. Figure 4.8 represents a typical clear summer day and Figure 4.9 represents a clear winter day. Below we describe some insights that may be observed from inspection of these data.

Figure 4.8
Clear-day aperture irradiance for different fixed and tracking aperture configurations for Albuquerque, NM on June 22.
Figure 4.9
Clear-day aperture irradiance for different fixed and tracking aperture configurations for Albuquerque, NM on December 22.Two-Axis Tracking Apertures
- The maximum amount of insolation is collected when a collector aperture points directly toward the sun, and hence the angle of incidence is zero. If a collector aperture can be tracked about two independent axes, the angle of incidence can be maintained at zero throughout the day.We show in Figures 4.8 arid 4.9 the beam aperture irradiance for a two-axis tracking aperture on the summer solstice and the winter solstice in Albuquerque, using insolation values calculated by the Hottel clear-day model. Also shown on the right-hand side of these figures is the daily aperture solar radiation energy. No method of concentration or tracking can increase these values since there is no cosine effect for a two-axis tracking aperture.
Single-Axis Tracking Apertures - If an aperture tracks the sun by rotation about a single axis, the beam aperture irradiance is reduced by the cosine of the angle between the tracking axis and the sun. This single tracking axis is often about a horizontal axis that can be oriented in any direction. The equation for the angle of incidence for these apertures was developed as Equation (4.12).
Figure 4.8 shows that in Albuquerque (35º latitude) in the summer, if the single axis is oriented in the north-south (N/S) direction, the reduction in beam aperture irradiance from the two-axis tracking case is minimal. As can be seen on the right-hand side, the difference between the day’s solar radiation energy on a N/S-oriented single-axis-tracking aperture and on a two-axis tracking aperture is only about 2 percent.
If the single tracking axis is oriented in the east-west (E/W) direction, the situation is different. For the E/W case, the only time the aperture points toward the sun is at noon. As the sun rises and sets, the cosine effect significantly reduces the rate of energy incident upon the aperture. Over the entire day, the amount of beam solar energy entering the aperture of the E/W single-axis tracker is only 73 percent of the energy that could have been collected if the cosine effect had been zero all day.
In the winter, as shown in Figure 4.9, the reverse is true. The performance of the E/W oriented single axis tracked aperture approaches that of the two-axis tracked aperture even in the morning and afternoon. In fact, the E/W tracking aperture receives 86 percent of the maximum amount of energy, whereas the N/S-oriented single -axis tracking aperture receives only 64 percent of the maximum solar energy for that day.
Taken over the entire year, the N/S-oriented single-axis-tracking aperture receives slightly more energy than does the E/W axis aperture. However, the variation of the daily irradiance over the year is much greater for the N/S axis orientation than for the E/W orientation.
If the demand for energy in a specific solar energy system design is higher in the summer than in the winter (i.e., for crop irrigation or cooling demands), this characteristic of the cosine effect on N/S tracking aperture as may be an advantage. If a somewhat constant demand is envisioned, however, the E/W orientation is usually chosen.
It is interesting that at noontime, the irradiance on the N/S-oriented single axis tracking aperture equals that on a horizontal fixed surface whereas the E/W-oriented single-axis tracking aperture irradiance equals that for a two-axis tracking aperture (i.e., the maximum possible). This is because at noon, the N/S single-axis tracker is pointing straight up and the E/W single-axis tracker is pointing directly at the sun. An examination of Equations (3.35) and (3.37) will convince the reader of this phenomenon.
Fixed Apertures The beam aperture irradiance for fixed-aperture collectors is also shown on Figures 4.8 and 4.9 for summer and winter in Albuquerque. The equation for the angle of incidence on fixed surfaces was developed as Equation (3.24). One of the surfaces shown here is horizontal and the other tilted up toward the south horizon by an angle equal to the local latitude. This orientation is often selected for flat-plate collector installations since it averages the noontime insolation peaks over the year.
A few points are interesting to note here also. First, a fixed horizontal surface receives more aperture solar radiation energy over the day (28 percent more in Albuquerque) than does a latitude-tilted, south-facing surface in the summer. In the winter, however, the horizontal fixed surface in Albuquerque receives only 49 percent of the daily energy that a latitude- tilted surface does.
4.2.4 Examples Using the TMY Database
Although a clear-day analysis of the cosine effect on apertures with different orientations and tracking capabilities is instructive, the most important solar radiation energy information to a system designer is the impact of tracking and collector orientation over a typical year with its varied insolation patterns. For example, in the winter, N/S-oriented single-axis tracking apertures receive much of their daily solar radiation energy in the early morning and late afternoon. If there were considerable morning and afternoon cloud cover in a particular climate, the performance of this tracking scheme would be even worse than predicted by our clear-day analysis.
Taking TMY beam insolation and applying the cosine of the appropriate angle of incidence to these data, we can develop a plot showing the variation of the monthly average aperture radiation energy over the year. Such a plot is shown in Figure 4.10 for Albuquerque, NM for the same apertures used in Figures 4.8 and 4.9. Even though typical weather data were used to produce these plots, trends similar to those noted before are shown to occur. Note the wide variation in the N/S single-axis tracking aperture solar radiation energy and the relatively constant solar radiation energy on the E/W single-axis-tracking aperture.

Figure 4.10
Monthly average and annual direct (beam) solar radiation energy incident on different fixed and tracking apertures using TMY data for Albuquerque, NM.The yearly average daily solar radiation energy on each aperture is shown on the right-hand side, indicating about a 9 percent difference between the E/ W and the N/S single-tracking axis orientation over the year. Note that the increase in aperture solar radiation energy over the year for providing a second tracking axis is about 17 percent for a N/S single-axis-tracking aperture. However, the penalty (relative to the N/S system output) for not tracking an aperture on even one axis is about 31 percent. It is obvious that the system designer must make some important choices as to the type of tracking and orientation of the solar collectors to be used in a system design.
4.3 Algorithm for Aperture Irradiance
We are now at a point where a computer code can be developed to predict aperture irradiance and solar radiation energy. Using the insolation models or databases discussed in Chapter 2 and applying the appropriate sun angle calculations developed here, we can make hour-by-hour computations of the solar energy entering the aperture of a collector. With appropriate summing, the daily aperture solar radiation energy may also be calculated.
In this section we describe the computer code APIRAD, which was written as an example of the use of the equations developed in Chapter 2, Chapter 3 and this chapter. In actual system design, a code similar to APIRAD would form a portion of the larger system design code package and provide the energy input to the collector model.
A flow diagram for a computer code for calculation of aperture irradiance and solar radiation energy is shown in Figure 4.11. Program APIRAD follows this diagram and calculates the beam irradiance and daily solar radiation energy on a collector aperture. This code is listed in the Appendix. The input data required are the day, the location, and the orientation of the collector and whether the collector is fixed or tracks the sun about one or two axes.
Since it doesn’t change rapidly, the declination angle may be calculated only once a day. Hourly calculations are then made of the hour angle and the sun’s altitude and azimuth. These values are used in the appropriate equation for the cosine of the angle of incidence.

Figure 4.11
Flow diagram for a general program that calculates beam aperture irradiance and solar radiation energy. Program APIRAD in Appendix H follows this sequence.Aperture irradiance is calculated once per hour and stored in an array AI (T), where the symmetry about solar noon is used to reduce the number of these computations. If real weather data were used, symmetry would not exist and full -day computations would be required. A test is made at sunrise to determine the daylight portion of that hour. The irradiance is then summed over the day through application of linear averaging between hours to give the daily aperture solar radiation energy.
The program uses the Hottel clear-day model to give the beam insolation component. Using Equation (2.15), we could include diffuse insolation and the global aperture irradiance would then be determined by applying Equation
(4.29). The program is not restricted to the use of the Hottel clear-day model. As noted in Figure 4.11, a different insolation model or an insolation database such as the TMY2 tapes could also be used.4.4 SHADOW - A Simple Model for Collector Field Shadowing
Typically, a solar thermal collector is not an isolated unit but, part of a large assemblage of collectors deployed on a field of finite dimensions. As a result, one collector may block (i.e., shadow) the sun, which would normally be incident on the aperture of another collector. Usually, enough land is provided so that the solar collectors can be spaced far enough apart to minimize shadowing. However, shadowing does occur, and the designer must be able to determine the appropriate field size on which to deploy the solar collectors.
Most computer programs used to analyze shadowing within a field of solar collectors are quite complex and require large computers for execution. However, a reasonable approximation of the impact of shadowing on collector performance can be obtained using a simple geometric model named SHADOW.
4.4.1 Parabolic Trough and Flat-Plate Collector Fields
The SHADOW model approximates the non-shadowed collector aperture area. The basic idea is that the total aperture area projected along a line pointing to the sun can never be greater than the field area projected along the same line. For a horizontal collector field, this can be expressed mathematically as
where:
Aa
= total collector aperture area (m2)Af
= collector field land area (m2)θi = angle of incidence between the sun’s rays and collector aperture
α = solar altitude angle
If the collector field land is not horizontal, the sine of the altitude angle must be replaced by the cosine of the angle between the sun’s rays and a normal to the field surface. To compute collector shadowing in a system performance model, we must incorporate the logic flow outlined in Figure 4.12.

Figure 4.12
Logic flow for the collector shadowing program SHADOW. In actual code, all computations are usually done as ratios of Aa/Af to provide a "per unit area" basis.As an example of the impact of shadowing on the amount of direct (beam) solar radiation energy incident on a collector’s aperture, Figure 4.13 was prepared for parabolic troughs having two different orientations. The use of the adjective non-first-row refers to the fact that in any collector field; one row of collectors will be non-shaded since there are no collectors between it and the line to the sun. Thus, for example, in an E/W parabolic trough collector field, the north row, is non-shaded when the sun is north of the east-west line whereas the south row is non-shaded when the sun is south of the east-west line.
Likewise, the east row in a N/S-oriented field of parabolic troughs is non-shaded before solar noon whereas the west row is non-shaded after noon. In order to use Figure 4.13, one must remember to also account for the front, non-shaded row. Similar plots could be generated for flat plates and dishes (if the field layout pattern is known) by using SHADOW as the basic computational tool.
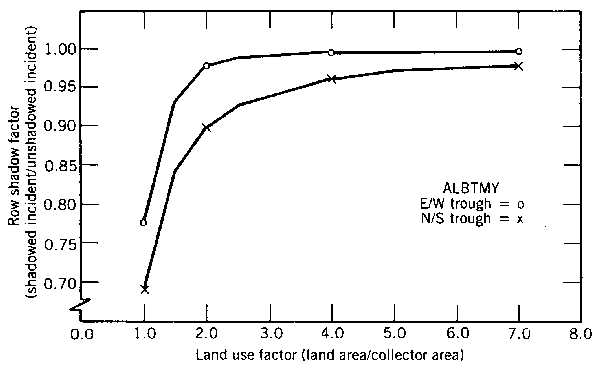
Figure 4.13
Non-first-row shading of annual direct (beam) solar radiation energy incident on parabolic trough collectors.EXAMPLE: Consider a N/S collector field containing two rows with a land use factor of 2.0. The annual direct (beam) solar radiation energy incident on the non-first-row collector is reduced to 0.895 (i.e., row shadow factor = 0.895 from Figure 4.13) of the non-shaded solar input. However, the annual direct (beam) solar radiation energy incident on the total field is reduced only (1.0 + 0.895)/2 or 0.948 that of the non-shaded field.
For parabolic dishes, the relationship in Equation
(4.32) must be modified slightly to account for the fact that circular dishes cannot be packed perfectly into a rectangular field, (this entire analysis assumes land is available in rectangular shapes suited for the deployment of solar collectors.)As shown in Figure 4.14 for dishes assembled in a diamond pattern, some space remains between the dishes even when they are packed together as closely as possible. In the layout represented in Figure 4.14, only 90.6 percent of the land area can be covered with dish aperture. Thus, for this case, Equation
(4.32) must be modified to
(4.33)
The factor of 0.906 will vary according to the dish layout chosen. Dishes deployed in a square pattern, for example, would have a factor of 0.785. Linn and Zimmerman (1979) discuss dish shadowing in some detail and provide a computer program to compute detailed shadowing within a dish field.

Figure 4.14
Land use for parabolic dishes deployed in a diamond patternTable 4.1 summarizes the angles developed so far, along with their zero value orientation, range and sign convention.
Table 4.1 Sign Convention for Important Angles
|
Title |
Symbol |
Zero |
Positive Direction |
Range |
Equation No. |
Figure No. |
|
Earth-Sun Angles |
||||||
|
Latitude |
|
Equator |
northern hemisphere |
+/- 90o |
--- |
3.3 |
|
Declination |
|
Equinox |
summer |
+/- 23.45o |
(3.7) |
3.5 |
|
Hour Angle |
|
Noon |
afternoon |
+/- 180o |
(3.1) |
3.3 |
|
Observer-Sun Angles |
||||||
|
Sun Altitude |
|
Horizontal |
upward |
0 to 90o |
(3.17) |
3.6 |
|
Sun Zenith |
|
Vertical |
toward horizon |
0 to 90o |
(3.8) |
3.6 |
|
Sun Azimuth |
A |
Due north |
clockwise* |
0 to 360o |
(3.18) or (3.19) |
3.6 |
|
Aperture-Sun Angles |
||||||
|
Angle of Incidence |
|
Perpendicular to aperture |
toward aperture |
0 to 90o |
(4.2) |
4.1 |
|
Aperture or Axis Tilt |
|
horizontal |
toward equator |
0 to 180o |
--- |
4.1 |
|
Aperture or Axis Zenith |
|
due north |
clockwise* |
0 to 360o |
--- |
4.1 |
|
Tracking Angle |
|
aperture normal vertical |
counter-clockwise* |
0 to 360o |
(4.8) |
4.2 |
|
Aperture Offset on Axis |
|
parallel to tracking axis |
counter-clockwise* |
+/- 90o |
--- |
4.6 |
* looking down + axis toward origin
References
Linn, J.K. and J.C. Zimmerman (1979), A Method for Calculating Shadows Cast by Two-axis Tracking Solar Collectors, Report SAND79-0190, Sandia National Laboratories, Albuquerque NM, November.
Zimmerman, J. C. (1981), "Sun Pointing Programs and Their Accuracy" Sandia National Laboratories Report SAND81-0761, September.