10.__________________________

  Central Receiver Systems

 

The central receiver concept for solar energy concentration and collection is based on a field of individually sun-tracking mirrors (heliostats) that reflect the incident sunshine to a receiver (boiler) at the top of a centrally located tower.  Typically 80 to 95 percent of the reflected energy is absorbed into the working fluid which is pumped up the tower and into the receiver.  The heated fluid (or steam) returns down the tower and then to a thermal demand such as a thermal electrical power plant or an industrial process requiring heat.

 

The basic difference between the central receiver concept of collecting solar energy and the trough or dish collectors discussed previously is that in this case, all of the solar energy to be collected in the entire field, is transmitted optically to a small central collection region rather than being piped around a field as hot fluid.  Because of this characteristic, central receiver systems are characterized by large power levels (1 to 500 MW) and high temperatures (540 to 840°C).

 

Central receiver technology for generating electricity has been demonstrated in the Solar One pilot power plant at Barstow, California.  This system consists of 1818 heliostats, each with a reflective area of 39.9 m² (430 ft²) covering 291,000 m² (72 acres) of land.  The receiver is located at the top of a 90.8 m (298 ft) high tower and produces steam at 516°C (960°F) at a maximum rate of 42 MW (142 MBtu/h).

 

System design for a central receiver application is performed in a manner similar to that when other types of collector are used.  Basically, the thermal output of the solar field is found by calculating collection efficiency and multiplying this by the solar irradiance falling on the collector (heliostat) field.  The balance of the system is then designed as discussed in the latter chapters of this book.

 

In this chapter we describe the components of a central receiver system and how they interact in a particular field design.  Then a computer model for collection efficiency is developed that can be used in conjunction with solar irradiance data and a system model such as SIMPLESYS to determine the system’s energy delivery capabilities.

 

• System Description
• Heliostats
• Receiver / Tower
• Field Layout
• System Thermal Performance
• Energy Losses
• System Performance Models
• SCRAM

 

The reader should realize that the material presented below represents the state-of-the-art for central receiver systems in the early 1980’s.  Since then there have not been any new central receiver power plants constructed, however the Solar One prototype power plant in Barstow underwent major modifications to test a different concept of central receiver design.

 

Renamed Solar Two, the facility at Barstow, CA was modified to test the concept of using molten salt as the heat transfer fluid rather than water/steam.  A completely new receiver was installed, and the storage was changed to a two-tank system.  In addition a few newly designed heliostats were added.  The Solar Two power plant was operated for over a year with generally positive results.  The reader is referred to the U.S. Department of Energy SunLab web site; http://www.sandia.gov/csp/csp_r_d_sandia.html  for current information on this technology.  For international status of central receiver technology, the reader is encouraged to go to the International Energy Agency Solar PACES web site; http://www.solarpaces.org/CSP_Technology/csp_technology.htm.

10.1   System Description

10.1.1   Heliostats

Design. The heliostat used in Solar One is shown in Figure 10.1. The reflecting element of a heliostat is typically a thin, back (second) surface, low-iron glass mirror.  This heliostat is composed of several mirror module panels rather than a single large mirror. The thin glass mirrors are supported by a substrate backing to form a slightly concave mirror surface.  Individual panels on the heliostat are also canted toward a point on the receiver.  The heliostat focal length is approximately equal to the distance from the receiver to the farthest heliostat.  Subsequent “tuning” of the closer mirrors is possible.

 

 

 

 

Figure 10.1   (a) Backside of the heliostat used at the Solar One central receiver pilot plant in Barstow, CA. (b) A photograph of the front of a Solar One heliostat (Both are courtesy of Southern California Edison Co.)

Another heliostat design concept, not so widely developed, uses a thin reflective plastic membrane stretched over a hoop.  This design must be protected from the weather but requires considerable less expenditure in supports and the mechanical drive mechanism because of its light weight.  Membrane renewal and cleaning appear to be important considerations with this design.

The reflective surface is mounted or supported on a pedestal that permits movement about the azimuth and elevation axis.  Movement about each axis is provided by a fractional-horsepower motor through a gearbox drive.  These motors receive signals from a central control computer that accurately points the reflective surface normal halfway between the sun and the receiver.  The equation for this half angle was developed in Chapter 8 as Equation (8.49).  The elevation and azimuth angles of a heliostat are given in Equations (8.52) and (8.53), respectively.

Heliostat Errors. A perfectly flat heliostat would produce an image on the receiver the size of the heliostat (projected normal to the heliostat-receiver direction) increased by the approximately 0.5 degree of sunspread.  For most applications, each mirror segment is concaved slightly and each mirror segment on a heliostat is canted toward a focal point.  This produces a higher flux density at the aim point.

A number of factors tend to increase the image size from a particular heliostat.  Mirror surface waviness is an important factor for heliostats as it is with parabolic collector surfaces. In addition, the gross curvature error of each mirror segment and the errors associated with accurate canting of each mirror segment on the heliostat frame further increase the image error. This last source of error can be amplified by the effects of differential thermal growth and gravity (heliostat position) on the heliostat frame.  All of these errors add up optically to produce a flux profile at the aim point (receiver) which has a distribution pattern similar to that shown in Figure 10.2.  The important heliostat performance parameter is the size of the isoflux contour containing 90 percent of the total reflected power.

Figure 10.2   Pattern of flux density arriving at the receiver from a typical heliostat.

In addition to producing a high flux density, the ability of the heliostat tracking system to position the centroid of the flux profile at the center of the receiver (aim point) is critical. Positioning errors may be caused by vertical and horizontal errors in the heliostat positioning or feedback mechanisms.  In addition, wind can produce structural deflections, causing position errors.

Most of the heliostat errors discussed become more significant (in terms of the flux “spilled” from the receiver), the farther the heliostat is located from the receiver. However, the flux contour and positioning errors are also critical for heliostats close to the tower because the projected area of the receiver is very small at that location.  A more complete discussion of heliostat errors and error measurement may be found in King (1982).

Environmental Considerations.  Probably the most important environmental design criterion that must be met by a heliostat design is the wind condition.  Typical requirements may be for the heliostat to meet its operating requirements in a 12 m/s (27 mph) wind, to survive a 22 m/s (49 mph) wind, and to continue to operate or move to the stow position in a 40 m/s (89 mph) wind (a position usually horizontal with mirrors face-up or face-down).  Also, the ability to survive hail is important for any flat surface exposed to the elements.  A typical hail survival criterion is 19 mm (0.75 in.) diameter hailstones impinging at 20 m/s (45 mph).

Tracking and Positioning. In order to keep parasitic energy use low, fractional horsepower motors with high gear rations are used to move the heliostat about its azimuth and elevation axes.  This produces a slow, accurate, and powerful tracking motion.  Under emergency conditions, however, rapid movement is an important design criterion. A typical minimum speed requirement would be that the entire field defocus to less than 3 percent of the receiver flux in 2 minutes.

 

Since it is currently considered best to stow the heliostats face-down during high wind, during hail storms, and at night, an acceptable time to travel to this position from any other position would be a maximum of 15 minutes.  The requirement for inverted stow is being questioned since it requires that the bottom half of the mirror surface be designed with an open slot so that it can pass through the pedestal.  This space reduces not only the reflective surface area for a given overall heliostat dimension, but also the structural rigidity of the mirror rack. However, face-down stow does keep the mirror surface cleaner.

10.1.2   Receiver-Tower

The receiver, placed at the top of a tower, is located at a point where reflected energy from the heliostats can be intercepted most efficiently.  The receiver absorbs the energy being reflected from the heliostat field and transfers it into a heat .transfer fluid.  There are two basic types of receivers: external and cavity.

External Receivers.  These normally consist of panels of many small (20-56 mm) vertical tubes welded side by side to approximate a cylinder.  The bottoms and tops of the vertical tubes are connected to headers that supply heat transfer fluid to the bottom of each tube and collect the heated fluid from the top of the tubes.

 

The receiver used at the Solar One facility is of the external type  and is shown in Figure 10.3.  It is located at the top of a 77.1 m (253 ft) tower and comprises 24 panels, each 13.7 m (45 ft) high, consisting of 70-12.7 mm (1/2 in.) diameter tubes.  Six of these panels are for preheating the water and 18 for producing steam.  This results in an overall receiver diameter of 7 m (23 ft). The tubes are made of Incoloy 800 and are coated on the exterior with high-absorptance Pyromark® black paint.

 

 

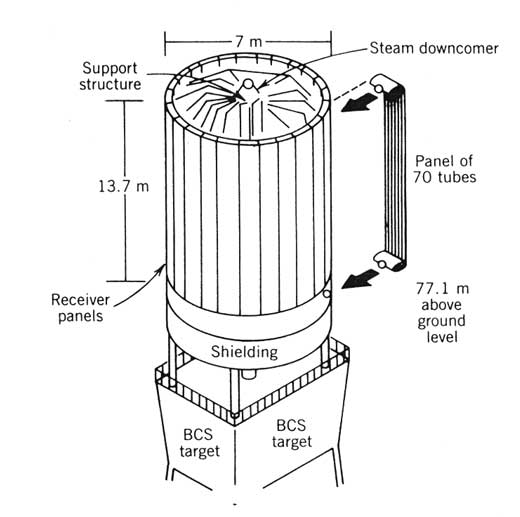
Figure 10.3   The receiver of the Solar One central receiver facility at Barstow, CA.  This is an external type receiver.

 

External receivers typically have a height to diameter ratio of 1:1 to 2:1.  The area of the receiver is kept to a minimum to reduce heat loss.  The lower limit is determined by the maximum operating temperature of the tubes and hence the heat removal capability of the heat transfer fluid.  or example, one design for a receiver using liquid sodium as the heat transfer fluid with peak output of 380 MW (1.3 × 109 Btu/h) calls for a height of 15 m (49 ft) and a diameter of 13 m (41 ft).  If the heat transfer fluid were water/steam or molten nitrate salt rather than sodium, an area about twice that size would be required for the same power output and temperature because of the lower heat transfer capabilities of these fluids (Battleson, 198l).

Cavity Receivers. In an attempt to reduce heat loss from the receiver, some designs propose to place the flux absorbing surface inside of an insulated cavity, thereby reducing the convective heat losses from the absorber.  An example of a cavity receiver design (with four cavities) is shown in Figure 10.4.  The flux from the heliostat field is reflected through an aperture onto absorbing surfaces forming the walls of the cavity.  Typical designs have an aperture area of about one-third to one-half of the internal absorbing surface area.  Cavity receivers are limited to an acceptance angle of 60 to 120 degrees (Battleson, 198l).  Therefore, either multiple cavities are placed adjacent to each other, or the heliostat field is limited to the view of the cavity aperture.

 

Figure 10.4   A cavity type receiver design incorporating four apertures.  It would operate in the 510 to 565oC (950 to 1050oF) temperature range with steam, molten salt or sodium (Battleson, 1981).

The aperture size is minimized to reduce convection and radiation losses without blocking out too much of the solar flux arriving at the receiver.  The aperture is typically sized to about the same dimensions as the sun’s reflected image from the farthest heliostat, giving a spillage of 1 to 4 percent.  For a 380 MW (1.3 × 109 Btu/h) plant design, the aperture width for the largest of the four cavities (the north-facing cavity) is 16 m (52 ft), and the flux at the aperture plane is four times that reaching the absorbing surface inside.

 

Heat Flux Considerations. The primary limitation on receiver design is the heat flux that can he absorbed through the receiver surface and into the heat transfer fluid, without overheating the receiver walls or the heat transfer fluid within them.  A survey of typical design peak values is given in Table 10.1.  The average flux over the entire absorber wall is typically one-half to one-third of these peak values.  Two other important considerations are: (1) limiting the temperature gradients along the receiver panels and (2) the daily heat-cycling of the receiver tubes.

 

Table 10.1  Typical Receiver Peak Flux Design Values

Source;  Battleson (1981).

Tower Design.  The height of the tower is limited by its cost.  The weight and windage area of the receiver are the two most important factors in the design of the tower.  Seismic considerations are also important in some locations.  The weight and size of a receiver are affected by the fluid choice as discussed previously.  Typical weights for a 380 MW (1.3 × 10⁹ Btu/h) receiver range from 250,000 kg (550,000 lb) for an external receiver using liquid sodium to 2,500,000 kg (5,500,000 lb) for a cavity air receiver.  These would be placed at the top of a 140 to 170 m (460 to 560 ft) tower if a surrounding heliostat field is used.

 

Proposed tower designs are of either steel frame construction, using oil derrick design techniques, or concrete, using smokestack design techniques.  Cost analyses indicate that steel frame towers are less expensive at heights of less than about 120 m (400 ft) and that concrete towers are less expensive for higher towers.  The results of such a cost analysis described in Sterns Roger Engineering (1979) are shown in Figure 10.5.

 

 

Figure 10.5  Tower cost data for towers of different heights.  The band reflects use of different receivers having different windage and weight.  These designs were made to withstand a 40 m/s (90 mph) wind and a ground acceleration of 0.25 g (Battleson, 1981).

 

Beam Characterization Targets. Prominent on any photograph or drawing of a central receiver tower are the white targets located just below the receiver. These are beam characterization system (BCS) targets used to aid in periodic calibration and alignment of individual heliostats.  They are coated with a diffusely reflecting white paint, and are not designed to receive the flux of more than one or two heliostats.  Instrumentation within the target area is used to determine the centroid and flux density distribution of the beam from a selected heliostat.  If the centroid of the beam is not located where the field tracking program predicts it to be, tracking program coefficients are modified appropriately.

 

Heat Transfer Fluids. The choice of the heat transfer fluid to be pumped through the receiver is determined by the application.  The primary choice criterion is the maximum operating temperature of the system followed closely by the cost-effectiveness of the system and safety considerations.  Five heat transfer fluids have been studied in detail for application to central receiver systems.  They are discussed separately in the paragraphs which follow.

 

The heat transfer fluids with the lowest operating temperature capabilities are heat transfer oils.  Both hydrocarbon and synthetic-based oils may be used, but their maximum temperature is around 425°C (797°F).  However, their vapor pressure is low at these temperatures, thus allowing their use for thermal energy storage.  Below temperatures of about -10°C (14°F), heat must be supplied to make most of these oils flow.  Oils have the major drawback of flammable and thus require special safety systems when used at high temperatures.  Heat transfer oils cost about $0.77/kg ($0.35/lb).

 

Steam has been studied for many central receives applications and is the heat transfer fluid used in the Solar One power plant.  Maximum temperature applications are around 540°C (1000°F) where the pressure must be about 10 MPa (1450 psi) to produce a high boiling temperature.  Freeze protection must be provided for ambient temperatures less than 0°C (32°F).  The water used in the receiver must be highly deionized in order to prevent scale buildup on the inner walls of the receiver heat transfer surfaces.  However, its cost is lower than that of other heat transfer fluids.  Use of water as a high-temperature storage medium is difficult because of the high pressures involved.

 

Nitrate salt mixtures can be used as both a heat transfer fluid and a storage medium at temperatures of up to 565°C (1050°F).  However, most mixtures currently being considered freeze at temperatures around 140 to 220°C (285 to 430°F) and thus must be heated when the system is shutdown.  They have a good storage potential because of their high volumetric heat capacity.  The cost of nitrate salt mixtures is around $0.33/kg ($0.15/lb), making them an attractive heat transfer fluid candidate.

 

Liquid sodium can also be used as both a heat transfer fluid and storage medium, with a maximum operating temperature of 600°C (1112°F).  Because sodium is liquid at this temperature, its vapor pressure is low.  However, it solidifies at 98°C (208°F), thereby requiring heating on shutdown.  The cost of sodium-based systems is higher than the nitrate salt systems since sodium costs about $0.88/ kg ($0.40/lb).

 

For high-temperature applications such as Brayton cycles, it is proposed to use air or helium as the heat transfer fluid.  Operating temperatures of around 850°C (1560°F) at 12 atm pressure are being proposed.  Although the cost of these gases would be low, they cannot be used for storage and require very large diameter piping to transport them through the system.

10.1.3   Field Layout

Decisions regarding the best position for locating heliostats relative to the receiver and how high to place the receiver above the field constitute a multifaceted problem, in which costs and heliostat “loss” mechanisms are the variables.  We first discuss some of these loss mechanisms and then how they interact in shaping an optimum heliostat field.

Cosine Effect.  The major factor determining an optimum heliostat field layout is the cosine “efficiency” of the heliostat.  This efficiency depends on both the sun’s position and the location of the individual heliostat relative to the receiver.  The heliostat is positioned by the tracking mechanism so that its surface normal bisects the angle between the sun’s rays and a line from the heliostat to the tower.  The effective reflection area of the heliostat is reduced by the cosine of one-half of this angle.  This may be visualized by considering heliostats at two positions in a field as shown on Figure 10.6.  Heliostat A has a small cosine loss since its surface normal is almost pointing toward the receiver.  Heliostat B has a larger cosine loss because of the position it must assume in order to reflect the sun’s rays onto the receiver.  Note that the most efficient heliostats are located opposite the sun.

 

 

Figure 10.6  The cosine effect for two heliostats in opposite directions from the tower.  For the noontime sun condition shown, heliostat A in the north field has a much greater cosine efficiency than does heliostat B.

 

An expression for calculation of the cosine of this half angle has been developed as Equation (8.49).  Incorporating the appropriate tower and heliostat position coordinates defined in Figure 8.20, we have

                                         (10.1)

where α and A are the sun’s altitude and azimuth angles, respectively, and z, e, and n are the orthogonal coordinates from a point on the tower at the height of the heliostat mirrors as depicted in Figure 8.20.

 

Field cosine efficiency, calculated by using Equation (10.1), has been plotted in Figure 10.7 for three sun altitude angles.  This figure also shows that the heliostats opposite the sun are the most efficient.  This is why most of the heliostats in a typical heliostat field (for an omnidirectional receiver) will be north of the tower.  In the morning, heliostats west of the tower will have a high efficiency and those east of the tower, a poorer efficiency.  The opposite occurs in the afternoon, giving the east and west fields an average efficiency in between the high and the low.

 

 

Figure 10.7  The cosine efficiency of heliostats at different field locations for three sun altitude angles.

Averaged over the entire year, the cosine efficiency of a field resembles that shown in Figure 10.8.  Again the north field dominance can be seen. In some de signs as Solar One in Barstow, California, the south field heliostats are used only to preheat the water, which is subsequently turned into superheated steam in the rest of the receiver.  This is done because of the reduced flux being reflected to this part of the receiver.

 

 

Figure 10.8  Annual average cosine efficiency at Barstow, CA (Holl, 1978).

Shadowing and Blocking. In previous chapters we discussed the problem of one collector casting a shadow on an adjacent collector, thereby reducing the energy output of the shaded collector.  For central receiver systems, there are two such interaction processes that reduce the amount of energy reaching the receiver.  These are shadowing and blocking by adjacent heliostats.

 

Shadowing occurs at low sun angles when a heliostat casts its shadow on a heliostat located behind it.  Therefore, not all the incident solar flux is reaching the reflector.  Blocking occurs when a heliostat in front of another heliostat blocks the reflected flux on its way to the receiver.  Both processes are illustrated in Figure 10.9.  Blocking can be observed in a heliostat field by noting reflected light on the backs of heliostats.

 

 

Figure 10.9  Shadowing and blocking loss of solar flux.

 

The amount of shadowing and blocking in a particular field layout is a function of the heliostat spacing, tower height, and sun angle.  Optimum field lay outs are made by use of ray tracing techniques in an extensive computer analysis.  These programs study representative heliostats in a field and check them for both blocking and shadowing by the heliostats in the two rows in front of the heliostat in question.  Two central receiver performance programs that have this capability are HELIOS (Biggs and Vittitoe, 1979) and DELSOL2 (Dellin et al., 1981).

 

This type of analysis is beyond the scope of this book; however, some general field layout guidelines have been developed from these studies.  It is generally best to arrange heliostats in a radial stagger pattern as shown in Figure 10.10.  This pattern minimizes land usage as well as shadowing and blocking losses.  The heliostats are tightly packed near the tower but must be sufficiently separated to prevent mechanical interference.  For heliostats located farther from the tower, the spacing increases in order to minimize blocking of the reflected beams.  Going out a long a radius, additional heliostats are added when spacing becomes too great and a new stagger pattern is established.

 

 

Figure 10.10  The radial stagger heliostat layout pattern developed by the University of Houston.

 

Heliostat packing density is the ratio of mirror area to field area.  The average heliostat packing density from optimized ray trace analyses of shadowing and blocking is typically in the range of 0.2 to 0.25 (Battleson, 1981).

 

Optimized heliostat layouts developed at the University of Houston (Lipps and Vant-Hull, 1978) have produced a means of determining spacing and average field density for preliminary field layouts.  The radial spacing ΔR and the azimuthal spacing ΔA, defined in Figure 10.10, are given by Dellin et. al. (1981) for high-reflectance heliostats (about 90 percent) in large fields as

        (10.2)

and

              (10.3)

where HM and WM are the height and width of the heliostat, respectively as depicted in Figure 10.9.  The angle θ_L is the altitude angle to the receiver from the heliostat location of interest and may be calculated as

                     (10.4)

where r is the normalized distance from the tower to the heliostat location measured in “tower heights.”

 

The local field density is the ratio of mirror area to land area at a particular point in the field.  This may be calculated as

                       (10.5)

where DM, the mirror density, is the ratio of mirror area to overall heliostat area.

 

The process of laying out a heliostat field consists of segmenting the land area around the tower into a number of concentric zones.  Equations (10.2) and (10.3) are used to determine the average or central radial stagger pattern within these zones, and Equation (10.5) is used to calculate the local field density. If large zones are selected, it may not be possible to maintain the azimuthal spacing defined in Equation (10.3) for all rings.  Heliostats near the inner ring of the zone may produce mechanical interference or unacceptable blocking or shad owing.  When this is the case, every fourth heliostat is normally removed from a ring in what is called a slip plane and the radial stagger pattern is restarted.

 

Figure 10.11 shows the spacing predicted by Equations (10.2) and (10.3). Note that for the heliostats farther from the tower, the radial spacing increases dramatically, whereas the azimuthal spacing decreases to the point where the heliostats at a particular radial distance have one heliostat width between them (ΔA = 2).  Figure 10.12 shows the decrease in local field density as distance from the tower increases.

 

 

Figure 10.11  Heliostat spacing for a field using the radial stagger layout pattern.

 

 

Figure 10.12  Local heliostat density as predicted by Equation (10.5) for radial-stagger field layouts.

Atmospheric Transmittance.  Many factors in field layout suggest that the field should extend far to the north of a very high tower.  One major limitation on the distance a heliostat is placed away from the tower is the attenuation of the reflected beam as it travels from the heliostat to the receiver.

 

Atmospheric transmittance has been approximated by Vittitoe and Biggs (1978) for a clear day (23-km visibility) and a hazy day (5-km visibility).  For a clear day with 23-km visibility, the atmospheric transmittance is

                (10.6)

where S is the slant range from heliostat to receiver in kilometers.  For a hazy day with only 5-km visibility, the atmospheric transmittance is

                                   (10.7)

Although these expressions were derived for a specific site altitude, they are strongly dependent on the aerosol distribution at ground level (visibility) and only slightly dependent on site altitude.

 

The effect of atmospheric attenuation is presented graphically in Figure 10.13.  The maximum slant range for Solar One is 0.44 km (1440 ft); however, larger fields are envisioned in the near future where atmospheric attenuation will be even more significant.

 

Figure 10.13  Atmospheric transmittance for a clear and a hazy atmosphere.

Optimization Studies.  A number of case studies have been performed that reflect optimum field layouts for the components studied (Battleson, 1981).  The shape of the optimum field depends on the power level of the plant.  For small systems of less than 100 MW (thermal), single or multiple north fields appear to be most economical. Any increase in power would require heliostats to be farther away from the tower. As the distance from heliostat to tower increases, atmospheric attenuation reduces the efficiency of the far-field heliostats.  This forces the placement of heliostats to the east and west of the tower in locations with lower cosine efficiency but less attenuation loss.  For large plants with power levels above 500 MW (thermal), the optimum field layout becomes a field surrounding the tower.

In addition to cosine loss and atmospheric attenuation, other performance tradeoffs are required to produce an optimum field.  These include spillage and receiver thermal loss as well as cost algorithms for the tower, piping, and receiver. The field designs resulting from these studies are shown in Figure 10.14. The height of the receiver tower for these fields falls into a range such as that shown in Figure 10.15.

 

 

Figure 10.14  Optimum field shape defined by cosine loss, atmospheric attenuation, tower cost, and other system performance parameters (Battleson, 1981).

 

 

Figure 10.15  Range of optimum receiver tower heights for systems with different power levels (Battleson, 1981).

 

10.2   System Thermal Performance

As with the solar collector modules discussed in the previous chapters, the thermal performance of a central receiver system may be defined in terms of an overall system efficiency.  It is common to define this efficiency in terms of the beam (direct) normal solar irradiance I_b,n and the total surface area of all of the heliostats in the field.  The overall energy collection efficiency of a central receiver system therefore is

                              (10.8)

where  is the rate of energy addition to the working fluid (measured at the bottom of the receiver tower), n_h is the total number of heliostats in the field, and A_h is the total area of the heliostat (based on outside dimensions, not the reflective portion).

 

In this section we discuss the modes of energy loss which make up the overall efficiency term η_col and then discuss how they are predicted.  We then discuss the large, detailed computer models available for performing such an analysis.  The section concludes with the presentation of a simplified model for calculating system performance that includes most of the important design variables.

10.2.1   Energy Losses

There are ten important sources of loss in a central receiver system that combine together to form the overall system energy collection efficiency.  These losses, cast in terms of efficiencies, may be allocated to either a field efficiency or a receiver efficiency. 

 

Table 10.2 lists the individual losses for a typical central receiver design and categorizes them either as part of the field efficiency or the receiver efficiency.  Example values are shown so that the reader can see the relative influence of each individual efficiency on the overall system performance.  The values shown are representative of a large, 380 MW (thermal) system in a mid-latitude desert climate using an external receiver and were taken from Battleson (1981).  For clarity, the percentage losses are shown.

Table 10.2. Central Receiver Energy Collection Losses

Source: Design study for a 380 MW (thermal) power plant (Sterns Rogers Engineering Company, 1979).

Field Losses. The energy losses associated specifically with the heliostat field include four of the five greatest sources of energy loss.  Most of these have been discussed in detail in the previous section.  The largest loss term is the cosine loss. As discussed in Section 10.1.3, cosine losses may be minimized through proper field design; however, they still represent the single most important loss mode.

 

Following the cosine effect in importance is the mirror reflectance loss.  Although new low-absorption glass mirrors can be made with a reflectance of about 94 percent, age and dust soon reduce this to an average value of about 90 per cent.  Keeping the mirrors washed, clean and in good repair is essential to maximize annual energy output.

 

The third most important loss factor for the losses listed in Table 10.2 is the atmospheric attenuation.  As discussed in the previous section, atmospheric attenuation becomes significant for very large heliostat fields where the outer heliostats are far from the receiver.  The value listed represents a large field having about 10 times the area of Solar One, where the atmospheric attenuation losses are estimated to be around 3 percent (Coggi and Eden, 1981).

 

Blocking and shadowing represent the next most important loss factor in central receiver system performance.  Although at noon, when the sun’s altitude is a maximum, there is usually no blocking or shadowing for a well designed field, significant blocking and shadowing does take place in the mornings and afternoons, especially in the winter, when the sun is low in the sky.  Because of this, the annual average blocking and shadowing losses are also significant.

 

Defining each of these losses in terms of an efficiency, we express the field efficiency as

 

                                              (10.9)

 

 

where η_cos, η_shadow, η_block, η_refl and η_atten are efficiencies (i.e., 1 minus the fraction of

energy lost in the process) based on cosine, shadowing, blocking, mirror reflectance, and atmospheric attenuation losses, respectively.

 

 

One loss source, receiver spillage, is a function of both the heliostat field (heliostat beam focus and distance from the tower) and the receiver (size of absorbing surface or aperture).  We have arbitrarily chosen to include this factor with the receiver loss rather than with the field loss.

Receiver Losses. The remainder of the losses tabulated in Table 10.2 are associated with the receiver.  The various modes of receiver loss are depicted in Figure 10.16.

 

 

 

Figure 10.16  Receiver heat loss modes.

Receiver efficiency may be defined as the product of each loss mode efficiency.

 

                                   (10.10)

 

where η_spill, η_absorp, η_rad, η_conv and η_cond are efficiencies based on receiver spillage, absorption, radiation, convection, and conduction losses, respectively.

 

The important energy loss for the receiver originates from convection and radiation heat transfer to the surroundings.  These losses depend on the design of the receiver, whether it is a cavity or external receiver, its heated (or aperture) area, and its operating temperature.  Additional factors include the local wind velocity, ambient temperature, and the orientation of the receiver.

 

Studies have been made on the combined radiation, free and forced-convection losses from large surfaces, and tilted cavities.  Siebers et al. (1982) have performed experiments on large vertical surfaces in horizontal f low, and their data are being used to predict losses from external receivers.  Clausing (1981) has developed a method for predicting the natural convective loss from cavity receivers.  A summary of these studies may be found in Siebers and Kraabel (1984).

 

Radiation and convection losses are primarily functions of the size of the receiver and the operating temperature of the system.  For most currently conceived central receiver system designs, the receiver operates at a constant temperature.  Therefore, the rate of energy being lost from the receiver is essentially constant throughout the day (and year) and the percentage loss increases in the morning and evening.  This makes the annual average percentage loss greater than the design point (noon) loss as indicated in Table 10.2.

 

It is this constant receiver thermal loss rate that defines the operating threshold for the system.  The system will operate only when the sun’s energy is sufficient to overcome the receiver heat loss.  This threshold usually occurs when the sun’s altitude angle is about 15 degrees.  Operation at sun angles below this is also constrained because of the rapid increase of heliostat blocking and shadowing.

 

Spillage loss or energy directed toward the receiver that does not fall on the absorbing area is a parameter of both the heliostat field and the receiver design.  The heliostat surface accuracy, beam spread, mirror canting accuracy, and tracking accuracy all have a major effect on the flux distribution at the receiver and, therefore, on the spillage.

 

Spillage loss can be reduced by increasing the size of the receiver.  The receiver is normally made large enough to intercept most of the reflected irradiance from the heliostat field and to keep peak incident flux values low enough for the heat transfer fluid. However, its size is limited because both radiation and convection heat losses are directly proportional to the receiver area.  Determination of the optimum receiver size requires numerous optimization studies with field receiver computer models.

 

In contrast to spillage, receiver absorptance is only a function of the type of coating on the absorbing surface. Many current designs use a high-absorptance paint commercially marketed as Pyromark®. This paint is formulated for high temperature surfaces and has an absorptance of approximately 0.95.  If the absorbing surface is inside a cavity, the effective absorptance (based on reflection back through the cavity aperture) increases to about 0.98.

 

The final receiver heat loss term represents the heat conducted away from the receiver. Most of this heat is lost through the receiver supporting brackets that connect the receiver to the tower structure. This is normally a small fraction of the total receiver heat loss and is kept small by minimizing the number and size of receiver attach points and using low thermal conductance metals such as stainless steels in their construction.

10.2.2   System Performance Models

For accurate prediction of the thermal performance of a central receiver system, it is necessary to define the flux profile produced on the receiver by a large number of representative heliostats throughout each day of a typical year.  This is done by the use of ray tracing and mathematical simulation techniques to determine the overall optical performance η_field and the spillage η_spill, of the central receiver system.

 

Three generally available models of this type are discussed here.  These were selected for their generality and universal availability.  Since they all require large, rapid computers for their operation, only a brief description is given here with references for further information.

 

HELIOS. The Helios optical behavior model was developed at Sandia National Laboratories in Albuquerque as a general simulation model for the optical behavior of reflecting concentrators.  The theoretical foundations on which this model is based are described in detail in Biggs and Vittitoe (1979).

 

The Helios model follows the incident solar irradiance through the system (including the intervening atmosphere) and includes all the factors that influence the optical performance of the collector.  An important output is the flux density pattern (W/cm²) at a grid of points on a surface (such as the receiver) and its integral over the surface.

 

The angular distribution of sun rays for the irradiance incident on a concentrator is modified by convolution, using a fast Fourier transform, to incorporate the effects of other nondeterministic factors such as sun tracking errors, surface s lope errors, and reflectance properties. Other analytical methods are used for beam statistics, off-axis reflecting optics, and atmospheric effects.

 

An optical performance computer program called HELIOS uses the Helios optical behavior model to predict the performance of real systems and is de scribed in Vittitoe et al. (1979).  This program has been used for performance predictions, safety studies, design tradeoffs, data analysis problems, specification and analysis of concentrator quality, and the general understanding of solar concentrator technology.

 

MIRVAL. This computer model was developed to perform the same type of analyses as HELIOS, but using a completely different optical modeling technique to perform its optical analyses.  This gives it the potential to analyze very complex but well defined systems.  The MIRVAL routine is described in Leary and Hawkins (1979).

 

DELSOL2. The DELSOL2 computer program calculated collector field performance and performs field layout and optimal system design for solar thermal central receiver plants.  It is described in detail in Dellin et al. (1981). The code consists of a detailed model of the optical performance, a simpler model of the non-optical performance, an algorithm for field layout, and a searching algorithm for determination of the best system design.  The latter two features are coupled to a cost model of central receiver components and an economic model for calculating energy costs.

 

The code can handle flat, focused, and/or canted heliostats and external cylindrical, multi-aperture cavity and flat plate receivers.  The program optimizes the tower height, receiver size, field layout, heliostat spacing, and tower position at the user specified power levels subject to flux limits on the receiver and land constraints for field layout.

 

10.2.3   SCRAM . An Approximation Model.

The overall thermal performance of a central receiver system can be predicted by using large, rapid, computer codes that require the specification of many design variables.  Most of the computational effort is associated with calculating blocking and shadowing losses.  Bergeron and Chiang (1980) have developed a mathematical approximation procedure that relies on data generated by the DELSOL2 code to determine many of the field optical performance parameters but is simple, rapid, and accurate.

This program, called SCRAM, may be used to perform many design tradeoff optimization studies such as storage sizing and load variation effects.  It may also be used for predicting long-term system performance when combined with a system simulation mode l (such as SIMPLESYS developed in Chapter 2 of this text) and realistic weather data (i.e., the TMY tapes discussed in Chapter 4).  The SCRAM model is simple enough for use on a microcomputer and is a useful tool for learning about the performance characteristics of a central receiver system.  The SCRAM algorithm has been reprogrammed in BASIC by the authors, and a copy of the code is included in the Appendix.

Description. The approach used in developing this code was to make use of DELSOL2 to generate a large amount of data that can be pictured as a surface in a multi-parameter space.  A polynomial function is found that is a good approximation to this surface over the range of parameters of interest.  The SCRAM program then uses these polynomials along with field layout and solar irradiance data to predict overall system performance.  The SCRAM approximation model can be considered an adjunct to DELSOL2.

 

The overall thermal energy collection efficiency of a point focus central receiver system, as defined by Equation (10.8), may be described in terms of the heliostat field efficiency and the receiver efficiency:

                       (10.11 )

where η_field was defined in Equation (10.9) and η_receiver in Equation (10.10). 

 

The SCRAM model accurately predicts the field efficiency and uses simple algorithms to determine receiver efficiency.  This is done to simplify the mathematics and may be justified on the basis that the dominant losses are contained in the field efficiency and that the assumptions used to evaluate receiver thermal efficiency are less reliable.  In the resulting model, receiver efficiency is computed directly and the algorithms used may be modified as a clearer understanding of receiver thermal losses develops.

 

A major simplification is introduced by recognizing that all the terms in the field efficiency, scale geometrically with tower height except for atmospheric attenuation, which is treated separately. Therefore, tower height is used as the unit length throughout the calculation until the final evaluation of the total power reflected toward the receiver is made.

 

Program SCRAM has been divided into two parts for operational ease.  The first part, SCRAM1, generates an array X_ij that is done only once for a specific heliostat field, Program SCRAM1 writes the values of this array on a disc naming the file XFILE.  Program SCRAM2 reads the data in XFILE along with sun angle and solar irradiance data to calculate the overall system performance.  This sequence is shown in Figure 10.17.

 

Figure 10.17  Program configuration for SCRAM.  Program SCRAM1 needs to be run only once for a particular heliostat field.

 

Fixed Parameters. Both the heliostat design configuration and the method of field layout are fixed for the SCRAM model presented here.  Modification of either of these would require multiple runs of DELSOL2 to generate a new set of surface fit coefficients C_i,j,k, which are specified in program statements 4020 through 4100.

 

The heliostat specified in this model has a rectangular reflecting surface 7.4 m (24.3 ft) × 7.4 m with focused, canted mirrors.  The mirrors do not have to cover the entire heliostat area.  Tracking errors and foundation motion are both assumed to be 0.75 mrad, and mirror waviness and panel alignment errors are both assumed to be 1.0 mrad. The canting and focusing values are the default values given in Section II of Dellin et al. (1981).

 

The field layout method specified for this model uses the radial stagger pattern with the University of Houston spacing parameters defined in Equations (10.2) and (10.3). The size and shape of the field can be varied.

 

SCRAM1 Input.  The size and shape of the heliostat field must be defined in SCRAM1 in terms of radial segments as shown in Figure 10.18.  The field is divided into JMX segments with ANG(I) (in radians) specifying the azimuth of the center line of each segment from north.  The distance from the tower to the innermost ring of heliostats in tower heights is RI(I), and the distance to the outermost ring is RO(I). Table 10.3 gives the program locations of these variables.

 

 

Figure 10.18  Heliostat field definition scheme for program SCRAM.  The program variables defining a field are shown.  For the field pictured, JMX =13.

 

 

Table 10.3.  Input Parameters for Program SCRAM

 

Notes:

·          The dimension statement for JMX must be changed if more than 13 segments are used.

·          An option is available (subroutine at statement 2000) to generate ANG(I), RI(I) and RO(I) for an eccentric circle field.

·          For angle SAA, zero azimuth is due south in SCRAM (rather than due north) for programming convenience.

 

In addition to the heliostat field configuration, several variable characteristics of the heliostats must be defined in SCRAM1.  The reflectance of the heliostat mirrors is a variable and is specified as MR.  Also, the ratio of mirror area to the full heliostat area may be varied by modification of DM. The total mirror area contained in the heliostat field, AM is the basic system sizing parameter and must be specified here.

 

The use of an atmospheric attenuation model and a receiver flux spillage model are both optional. The optical attenuation model is that given in Equation (10.6).  As noted, this model represents the terrestrial propagation loss for a clear day.

 

An approximate spillage model may also be used.  This has been developed from DELSOL2 results of optimally designed fields.  The receiver is a cylinder that has a diameter and height of 0.091 tower heights.  The receiver spillage model is described in Appendix C of Bergeron and Chiang (1980).

 

SCRAM2.  This portion of the program requires the input of receiver loss parameters, solar irradiance, and sun position data.  Receiver loss is characterized by two variables, receiver absorptance ROPT and total receiver heat loss rate RTHER.  Receiver absorptance depends on the radiation characteristics of the surface or the cavity.  A representative value of 0.87 is used in the listing of the program.

 

Because most receivers are designed to operate at constant temperature, the receiver heat loss is assumed constant throughout the day.  As a first approximation, the receiver heat loss may be estimated by

                      (10.12)

where U_l, is approximately 35 W/m² K (6.2 Btu/h ft² F), A_r  is the receiver surface area (or aperture area in the case of a cavity receiver), and (T_out - T_a ) is the temperature difference between the fluid outlet temperature and the average daytime ambient temperature.  If the receiver surface area is not known, it may be roughly approximated by assuming that the system has a geometric concentration ratio of about 250.

 

Solar position and solar irradiance data are also input to SCRAM2.  The sun ‘s zenith angle is input as SPA, and the azimuth as SAA.  For programming convenience, the azimuth zero is due south rather than due north as used throughout the remainder of this book.  The direct normal solar irradiance in W/m² is input as DN.  All of these parameters vary throughout the day and year; therefore, when configured for long-term performance calculations, SCRAM2 would read these solar input parameters from a large array.

SCRAM2 Output.  The important parameter calculated by SCRAM2 is the field efficiency (ETA/AM).  This is defined as the ratio of the radiant power incident on the receiver to the solar power incident normal to an area equal to the mirror area.  It should he emphasized that this efficiency is not based on the land area covered, but on the total heliostat aperture area.

 

The total power reflected to the receiver (PWR) is simply the product of field efficiency, the total reflective surface area, and the direct normal solar irradiance.  The total power output (POUT) to the working fluid is then calculated by applying the receiver surface absorptance and total heat loss rate that had been input into the program.  A collection efficiency (ECOL) equivalent to that discussed for other collectors is calculated as the ratio of the power into the working fluid to the direct normal solar irradiance on the heliostats.

Example.  The input data for an example case are contained in the program listing in the Appendix.  The case defined is for a heliostat field that has a total mirror area of 75,000 m² (246,000 ft²).  The heliostats have a reflectance of 89 percent, and mirror coverage (density) is 89.7 percent.

 

The heliostat field is defined by using the eccentric circle option with the outer circle having a radius of 5 tower heights.  The inner circle has a radius of 0.5 tower heights with its center displaced to the south by two tower heights.  This field configuration is pictured in the insert to Figure 10.19.

 

Figure 10.19  Performance of an eccentric circle central receiver field for the example above and calculated with the use of program SCRAM.

The receiver’s absorptance was assumed to be 0.87 and its thermal loss was estimated to be 9.5 MW/m².  Both the atmospheric attenuation model and the receiver spillage model discussed previously were used in the calculations.

 

Variation of the field efficiency (neglecting receiver losses) as the solar zenith angle changes is shown in Figure 10.19.  Data for three sun azimuths are shown.  The highest efficiencies occur when the sun is due south of the field (SAA = 0).  As the sun comes around toward the west, the field efficiency decreases, and the limiting (impossible) case occurs when the sun is due north of the field.

 

For each azimuth, however, the peak field efficiency does not occur when the sun is directly overhead (SPA = 0).  Instead, this peak occurs when the sun’s zenith angle is between 15 and 30 degrees.

 

The minimum field efficiency occurs at large sun zenith angles, that is, when the sun is low in the sky and shadowing is significant.  However, it is interesting that for the field shown, the field efficiency remains high (50 percent for 270 degree azimuth) even when the sun is 15 degrees above the horizon.

 

The central receiver design described above was used along with typical meteorological year (TMY) data for Albuquerque, New Mexico to illustrate the use of SCRAM1 and SCRAM2.  Performance for one day (June 20) near the summer solstice is shown in Figure 10.20.  The rates of energy incident on the heliostats, reflected to the receiver, and entering the working fluid are shown.  Field efficiency and system collection efficiency are also shown for this case.  If this computation is performed for every day of the year with the use of TMY solar irradiance data, the total yearly thermal energy delivered by the system will be computed. This is the most important issue for the system designer.

 

 

Figure 10.20   System performance calculated by SCRAM2 for a 75,000 m2 central receiver system located in Albuquerque, NM on June 20 using TMY solar irradiance data.

Program SCRAM2 may also be used as a subroutine to SIMPLESYS.  In that case, SCRAM2 would replace statements 420 through 550 of SIMPLESYS with QC (in SIMPLESYS) being set equal to POUT (in SCRAM2) and the final GOTO statement in SCRAM2 removed.

References

Battleson, K.W.(1981), “Solar Power Tower Design Guide: Solar Thermal Central Receiver Power Systems, A Source of Electricity and/or Process Heat,” Sandia National Labs Report SAND81-8005, April.

Bergeron, K. D., and C. J. Chiang (1980), “SCRAM: A Fast Computational Model for the Optical Performance of Point Focus Solar Central Receiver Systems,” Sandia National Labs Report SAND80-0433, April.

Biggs, F. and C. M. Vittitoe,(1979), “The HELIOS Model for the Optical Behavior of Reflecting Solar Concentrators," Sandia National Labs Report SAND76-0347, March.

Clausing, A. M. (1981), “An Analysis of Convective Losses from Cavity Solar Central Receivers,” Solar Energy 27 (4), 295.

Coggi, J., and H. Eden (1981), “Solar 10 Megawatt Pilot Plant Performance Analysis,” The Aerospace Corporation, Report No. ATR-81 (7747)-1, February.

Dellin,T.A., M. J. Fish, and C. L. Yang (1981), “A User’s Manual for DELSOL2: A Computer Code for Calculating the Optical Performance and Optimal System Design for Solar Thermal Central Receiver Plants,” Sandia National Labs Report SAND81-8237, August.

Holl, R. J. (1978), “Definition of Two Small Central Receiver Systems,” Sandia National Labs Report SAND78-7001, April.

King, D. L. (1982), “Beam Quality and Tracking Accuracy Evaluation of Second Generation and Barstow Production Heliostats,” Sandia National Labs Report SAND82-0181, August.

Leary, P., and J. Hawkins (1979), “A Users Guide for MIRVAL Computer Code for Comparing Designs of Heliostat Receiver Optics for Central Receiver Solar Power Plants,” Sandia National Labs Report SAND77-8280, February.

Lipps, F. W., and L. L. Vant-Hull (1978), “A Cellwise Method for the Optimization of Large Central Receiver Systems,” Solar Energy 30(6), 505.

Siebers, D. L., and J. S. Kraabel (1984), “Estimating Convective Energy Losses from Solar Central Receivers,” Sandia National Labs Report SAND84-8717, April.

Siebers, D. L., R. G. Schwind, and R. J. Moffat (1982). “Experimental Mixed Convection From a Large, Vertical Plate in a Horizontal Flow,” in Proceedings of the Seventh International Heat Transfer Conference, Munich, vol. 3, pp. 477-482, September 6-10.

Sterns Roger Engineering Company (1979), “Tower Cost Data for Central Receiver Studies,” Sandia National Labs Report SAND78 -8185, June.

Vittitoe, C. N., and F. Biggs (1978), “Terrestrial Propagation Loss,” paper presented at the American Section, International Solar Energy Society Meeting, Denver, Colorado, August.

Vittitoe, C. N., F. Biggs and R. E. Lighthill (1979), “HELIOS: A Computer Program for Modeling the Solar Thermal Test Facility, A Users Guide,” Sandia National Labs Report SAND76-0346, March.